マスコミの方々も科学への理解力を養ってください!
2001年4月19日
宇佐美 保
オームの松本サリン事件で、科学への理解不足から、お気の毒な河野さんを犯人呼ばわりしてしまったマスコミの方々は、その後も科学への理解力を高める努力を全くしていません。
なのに、教科書で円周率は、3.14……でなく、3として教えることには、声を大にして反対しています。
でも、彼らは、円周率を3.14……でなく、3とするとどうなるかを理解していないのです。
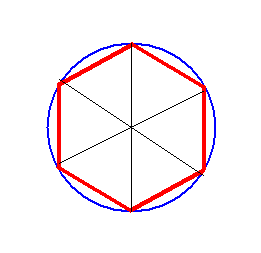 左図の(青い)円の周囲(円周)と、(赤い)六角形の周囲(外周)とでは、誰が見ても円周の方が長い事は判る筈です。
左図の(青い)円の周囲(円周)と、(赤い)六角形の周囲(外周)とでは、誰が見ても円周の方が長い事は判る筈です。
しかし、円周率を3にしてしまうと、右図の円周と六角形の外周の長さは同じになってしまうのです。
何故なら、この(赤い)六角形は右図のように六個の正三角形に分割できます。
そして、正三角形は三辺の長さはすべて同じですから、正六角形の外周の長さは(三角形の一辺の長さ)×6です。
一方、円周は(直径)×(円周率)=(半径)×2×(円周率)
ここで、(半径)は右図を見てお判りのように(三角形の一辺の長さ)と同じで、それに何しろ円周率は3なのですから、
円周=(三角形の一辺の長さ)×6 となり、図の青い円の円周と、赤い正六角形の外周とは同じ長さになってしまうのです。
この事実を是認するならば、「或る二点を最短距離で結ぶのは直線である」という絶対的な公理と矛盾してしまうのです。
何しろこれらの正六角形と円との隣り合う接点同士を直線で結ぼうが円弧を描いて結ぼうと同じ長さだというのですから!
こんな事を、学校で押し付けられてしまう子供達は可愛そうです。
一月位前だったでしょうか?
テレビ朝日のニュースステーションに、中村修二氏(青色発光ダイオードの開発に成功して、ノーベル賞に最も近い日本人と言われている方)がゲストで登場して、“学校教育に於いては、全ての科目を習得する必要はなく、好きな科目に打ち込めば良い!なにしろ、一つ事で長じた後は、他の事を習得するのは容易となるのだから。”旨を語られました。
この言葉は、久米キャスターも、コメンテイタで朝日新聞論説委員の清水建宇氏も、よほど気に入られたようで、久米氏は己の科学的無知さ加減の良い口実としています。
更に調子に乗った清水氏は“学校では、読み書き算盤だけを教えるくらいで良い。”とさえ言い出しています。
ところが、この算盤勘定も彼らには苦手なようです。
今度は、ニュースステーションのゲストで日刊スポーツの野崎氏が登場して、セ・リーグが今季から優勝球団を決める際に「勝利数1位」と「勝率1位」が異なった場合プレーオフを行うのだと語っていました。
なにしろ、以前、セリーグに於いて(多分1986年の広島の優勝の時と思いましたが?)、1シーズン各チームが同一試合数を戦い終わった後、当然、勝率一位のチームの優勝となったのですが、ところが勝利数では2位チームの方が多かったのだそうです。
このように、1シーズン同一試合数を戦ったチーム間に、「勝利数1位」と「勝率1位」が存在するなんて、おかしな事なのですが、この原因は、日本のプロ野球では、勝率を計算する際に、引き分け試合をノーゲームとして処理しているからです。
ですから、勝利数が少なくても、引き分け数が多ければ、勝率が向上して優勝さえしてしまうのです。
そこでインターネットでセリーグの年間成績を調べましたら、
|
暦 |
優勝チーム |
試合 |
勝利 |
敗戦 |
引分 |
勝率 |
ゲーム差 |
2位チーム |
|
1986 |
広島東洋カープ |
130 |
73 |
46 |
11 |
.613 |
0 |
巨人 |
の結果を得られました。
尚、この広島の勝率0.613は当然次式で導いているのです。
(勝利数)÷(全試合数−引き分け試合数))=73÷(130−11)=73÷119=0.61344537815126050420168067226891≒0.613
(この年の巨人の勝利数などの記録は私には調べられませんでした)
但し、ゲーム差が0で、広島が73勝、46敗なのですから、巨人はこの上に、(例えば、5割の勝率で)1勝1敗、2勝2敗、3勝3敗、4勝4敗、5勝5敗と、勝ち数と負け数と同じ数を上積みしていると考えて、これらの場合について、巨人の勝率を計算してみます。
|
巨人の上積み分 |
巨人の引き分け数 |
勝利数 |
全試合数−引き分け試合数 |
勝率 |
|
1勝1敗 |
9 |
74 |
121 |
0.612 |
|
2勝2敗 |
7 |
75 |
123 |
0.610 |
|
3勝3敗 |
5 |
76 |
125 |
0.608 |
|
4勝4敗 |
3 |
77 |
127 |
0.606 |
|
5勝5敗 |
1 |
78 |
129 |
0.605 |
この表をご覧頂きますと、「勝利数」が増えれば増えるほど勝率は下がって行きます。
従って、(引き分け試合無しで)73勝46敗(73÷(73+46)=0.603)と5割以上の勝率で来ていた後に、1勝1敗の5割で試合を進めてゆけば、当然勝率は下がって行くのです。
ところがもう一度繰り返しますが、(引き分け試合無しで)73勝46敗まで来て、その後引き分けを続けて行っても勝率は下がらないのです。
(参考の為に、ゲーム差に囚われずに、巨人が広島に対して、勝ち数が1つ、負け数は同じ(となると引き分け数は10)だったとしますと、このときの勝率は、
74÷(130−10)=74÷120=0.617
となり、同じ勝ち数でも、勝率は変わり広島を上回ります。)
何故このような事態になるのでしょうか?
この背景には、引き分け試合の取り扱い方が、異常なのです。
一般社会の通念として、引き分けは0.5勝(0.5敗)として扱えば良いのです。
ところが、日本のプロ野球の規則では、引き分け試合を勝率計算から除外しています。
この制度は一見、実に合理的なようなのですが、とんでもない悪制度なのです。
と言うのはこの制度下では、引き分けの価値は、0.5勝でなく、そのシーズンの最終勝率の価値を有してしまうのです。
ですから、最終勝率0.613で優勝した広島にとっては、(11の引き分け試合全て)引き分けは0.5勝でなくて、0.613勝の価値があったのです。
マスコミは、日刊スポーツの野崎氏をはじめ、日本語の使い方が出鱈目の長嶋氏さえも、「勝利の方程式」等と数学用語を使っていますから、この件を、簡単な方程式で説明しましょう。
先ず、全試合数をZ, 勝利数をK、 (前数をM) 引き分け試合数をH、
勝率(現時点での日本プロ野球の計算方法に基づく)をR としますと、
R=K÷(Z−H)
ここで、引き分け試合の勝ち数への換算率をXとしますと、
Z試合での勝ち星数は、K+H×X となります。
ですからこの勝ち星数をZで割った新たな勝率は、先に表した勝率R=K÷(Z−H)と等しくなるのです。
従いまして、(K+H×X)÷Z=K÷(Z−H)
これを解きますと、簡単に、X=
K÷(Z−H)
即ち、「引き分けの価値はシーズンの最終勝率」が得られます。
そこで、広島の73勝46敗11引き分けを、引き分けの価値を0.5勝として計算しなおすと、広島の換算勝ち数は、73+(11×0.5)=78.5
従って、勝率は、78.5÷130=0.604
一方、巨人が74勝7敗9引き分けとすると、
換算勝ち数は、74+9×0.5=78.5と広島と同じとなり、当然勝率も同じとなります。
ですから、広島と巨人は優勝決定戦を行うべきです。
このように、引き分けは0.5勝という一般常識を導入すれば、『セ・リーグは今季から優勝球団を決める際に「勝利数1位」と「勝率1位」が異なった場合プレーオフを行う』などという訳の判らない制度を打ち立てる必要は無いのです。
こんな理不尽の事を日本のプロ野球は平気で行っているのです。
そして、この日本のプロ野球を“自分は、中央公論に入社したかったが、入社試験が一番だった為に落とされた。”とか、“前立腺の手術のための入院の際は、量子力学……などの本を持ち込んだ。”とかいった具合に、己の頭脳を自慢するような人物たる読売新聞社のナベツネなる人物が牛耳っているのです。
なのに、何故彼はこの不合理に気が付かないのでしょうか?
多分彼の頭脳は、彼の思っているほどは優れていないのでしょう。
こんな事が、そして、巨人優位なドラフト制度などが、罷り通ってしまう日本プロ野球は、世界の笑いものです。
又この点を正しく指摘出来ないマスコミには困ったものです。
中村修二氏が指摘した“学校教育に於いては、全ての科目を習得する必要はなく、好きな科目に打ち込めば良い!”の趣旨は、“一芸に長ずれば、多芸に通ず。”なのであって、日本人社会での通念の「文系の人間は理系には疎く、理系の人間は文系に疎い」を是認しているのではないのです。
理系の人間でもその分野で長ずれば、当然容易に文系にも通じる事が容易であると言っているのです。
従いまして、いつまで経っても、文系分野しか判らず理系には無知であるマスコミの方々は、当然彼らは彼らの分野で長じている存在ではないのだと自覚すべきでしょう。
又、理系への理解をサボっているだけなのです。
(文系理系なんて、いつ誰が区別し始めたのですか?)
勿論、文系理系に留まらず、同じ理系の中で、機械屋、電気屋、化学屋などと一生自分の看板を後生大事に掲げて他分野への無知を正当化している方々への警告でも有るのです。
(補足)
何と言われようと方程式はどうも苦手でよく判らないとおっしゃる方も居られましょうから、次のような極端な場合を考えてみましょう。
130試合を戦い抜いた後の次のA,B,CそしてDチームの勝率を、引き分け試合を勝率計算から除外するという、現在の日本プロ野球の勝率計算方式で求めてみます。
(余りに簡単な例なので、計算するまでもないのですが。)
Aチームは130勝0敗0引き分け、
この場合は当然、勝率は130/130=勝率10割
Bチームは1勝0敗129引き分け、
この場合も(不思議な事に)、1/(130-129)=1/1=勝率10割
Cチームは0勝1敗129引き分け、
この場合は(一寸不思議な事に)、0/(130-129)=0/1=勝率0割
Dチームは0勝130敗0引き分け、
この場合は当然、勝率は0/130=勝率0割
やはり可笑しいでしょう?
(勿論、6チームで戦っていたらこのような事にはなりませんが、全世界(130チームではきかないでしょう)の野球チームで1戦づつ戦っていたらこんなことになるかもしれません。)
この原因は、「引き分けを勝率計算から除外する」と云っても、実質的な除外ではなく、前述の如く、引き分けを除いた勝率分を引き分け試合の価値に与えてしまっているのです。
即ち、Bチームには引き分けの価値は1勝分、Cチームには0勝分。
従って、Bチームの勝率は、(1+(129×1.0))/130=130/130=10割
Cチームは残念ながら、勝率は、(1+(129×0.0))/130=0/130=0割
しかし一般常識では、引き分けの価値は0.5勝ですから、
Bチームの勝率は、(1+(129×0.5))/130=65.5/130=5.04割
Cチームの勝率は、(0+(129×0.5))/130=64.5/130=4.96割
この結果の方がやはり一般的常識に適っているのではないでしょうか?